20210511

回顾

恋词复习

• intricate adj.错综复杂的；难理解的
• sacred adj.神圣的；宗教性的；庄严的
• resemble v.像；类似于
• analogous adj.相似的；类似的
• superfluous adj.过剩的；多余的
• superficial adj.表面的；肤浅的；浅薄的
• substitute n.代替者；代替物；替补 v.用..代替；取代

离散数学-判断某非负整数列是否能简单图化

首先用必要条件去试试

1. 奇数度结点度数之和是否为偶数
2. 无向图顶点度数之和是否为边数的2倍

然后就是用Havel定理（这个真好用！）且这个是充要条件。大概步骤是这样的

1. 对已知的度数列进行降序排列（相等的放在一起）。
2. 假设最大的度为k（已经排在首位），删去最大的度数k，对后面的k个度数都进行减1，再进行降序排列，由此得到一个新度数列。
3. 重复第2步的操作。
4. 若在此期间出现了负数，则不是简单图；若最后剩下的度数列的度数均为0.则为简单图。

举几个例子就懂了！

• 5,4,3,2,2

• 5,5,4,4,2,1

• 3,3,3,1

3,3,3,1;
//删掉最大的度3，对后面3个度数都减1
↓
2,2,0;
//删掉最大的度2.对后面2个度数都减1
↓
1,-1;   //出现了负数，不是简单图

• 4,4,3,3,2,2

4,4,3,3,2,2;
//删掉最大的度4，对后面4个度数都减1
↓
3,2,2,1,2;
//此时不是降序排列，则重新排列
↓
3,2,2,2,1;
//删掉最大的度3，对后面3个度数都减1
↓
1,1,1,1//
//删掉最大的度1，对后面1个度数都减1
↓
0,1,1;
//此时不是降序排列，则重新排列
↓
1,1,0;
//删掉最大的度1，对后面1个度数都减1
↓
0,0;
//最后剩下的度数列的度数均为0.则为简单图。

线性代数-线性方程组（一）

不知不觉来到了第四章，这一章是考试的重点，mark一下。

• Ax = 0
  • 基础解系
  • n-r(A)
• Ax = b
  • 有解判定
  • 解的结构
• 方程组应用
• 公共解，同解

--

数据结构-最小（代价）生成树-最短路径-图（三）

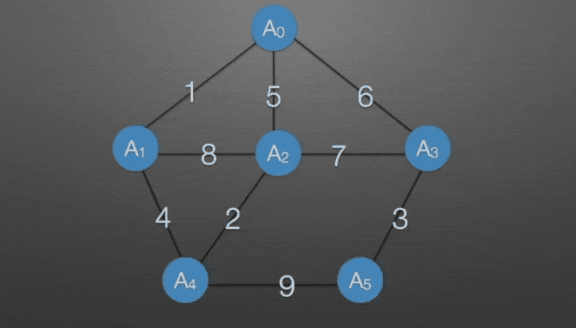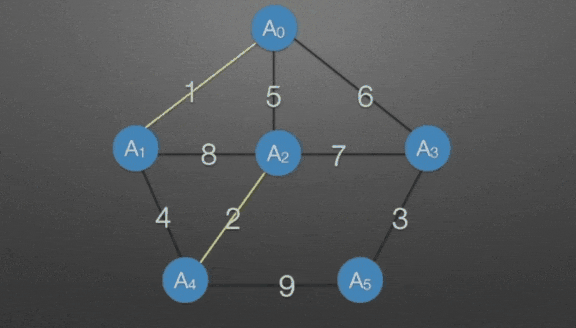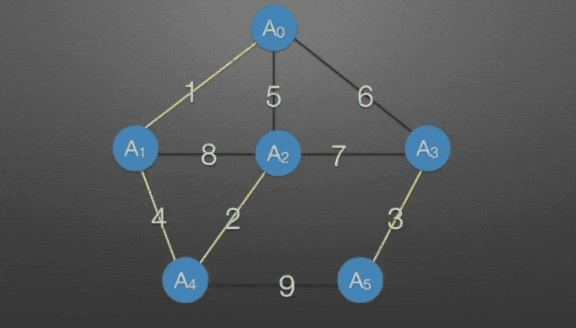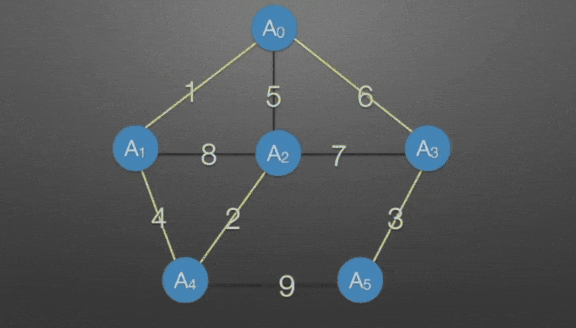
普里姆算法（Prim）

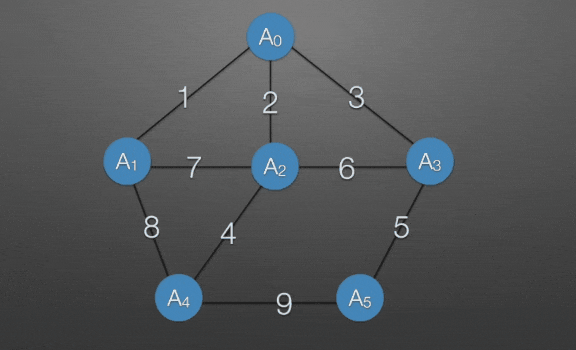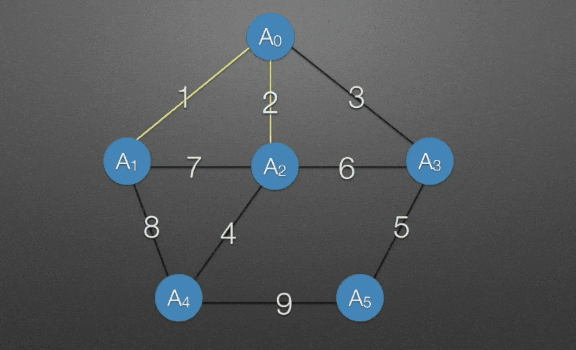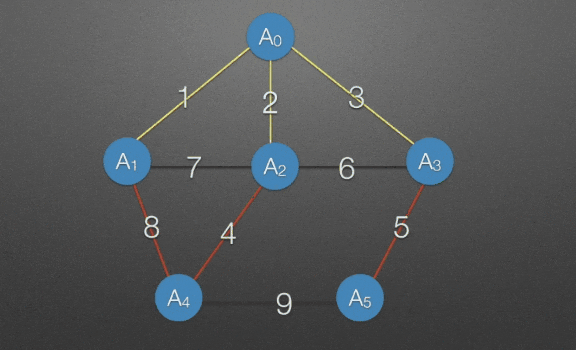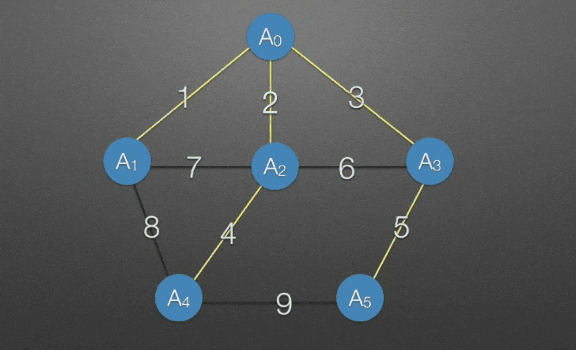
选出A，把A0并入生成树中
→ 找出与之相邻鹅所有边即长度为1，2，3的边，显然为长度为1的边，将A与长度为1的边并入生成树中
→ 找出A0,A1相邻的所有边：8，7，2，3，选2，将A2与2并入
→ 找出A0,A1,A2相邻的所有边：8，4，3，6，7，7舍掉，因为选7会形成环就不是树了。选3，将A3与3并入
→ 找出A0,A1,A2,A3相邻的所有边：8，4，5，选4，将A4与4并入
→ 找出A0,A1,A2,A3,A4相邻的所有边，5，9，选5，将A5与5并入

克鲁斯卡尔算法（Kruskal）

哪条边最短？
→ 权值为1的那条，并入
→ 权值为2的那条，并入
→ 权值为3的那条，并入
→ 权值为4的那条，并入
→ 权值为5的那条，不能并入，会形成环
→ 权值为6的那条，并入

每次选未被并入且不会产生环的最短的边进行并入。 那么如何检查会不会产生环？ → 并查集 → 查找是否为同一个根结点。

迪杰斯特拉算法（Dijkstra）

弗洛伊德算法（Floyd）

恋词U15

• retrospect n.回顾；回想
• spectrum n.光谱；波谱；范围；各层次
• blaze n.火焰；烈火
• boast v.自夸；自吹子列
• booth n.公用电话亭；岗亭；摊位
• soar v.指鸟翱翔；猛增；高耸
• celebrity n.名望；著名；名人
• combat v.与..斗争；防止；减轻 n.战斗；斗争；格斗
• shed some light on 弄清楚；解释；说明
• come to light 为人所知；暴露
• tight-lipped adj.守口如瓶的；紧闭双唇的
• phase n.阶段；时期
• nasty adj.讨厌的；下流的；危险的
• psychiatry n.精神病学；精神病疗法
• auction n.拍卖
• prestigious adj.有威望的；声誉高的
• revive v.使苏醒；复活；复苏
• advisory adj.顾问的；咨询的
• collective n.集体；团体；集体企业 adj.集体的；共同的
• eligible adj.有资格；合意的；中意的