Table of Contents
回顾
- corporate adj.公司的;法人的;全体的;共同的
- incorporate v.把..合并;使并入;混合;包含
- manual adj.手工的;人力的;手动的
- subconscious adj.下意识地;潜意识的
- heal v.使治愈;愈合;和解
- pharmaceutical [ˌfɑ:məˈsu:tɪkl ]adj.制药的
- aviation n.航空;飞行
- aesthetic adj.美学的;艺术的;审美的
- intricate adj.错综复杂的;难理解的
数据结构-图的遍历-图(二)
从图中的某一顶点出发,访遍图中其余顶点,且使每一顶点仅被访问一次,这一过程就叫做图的遍历(Traversing Graph)
图的遍历算法-深度优先搜索遍历(DFS)
深度优先遍历(Depth First Search),也有称为深度优先搜索,简称为DFS。类似于树的前序遍历
想象一下,此时站在A处(其他也可以),(面向D的方向)。给自己定一个原则,右手原则(或左手原则也可以),从A开始要走遍所有的图顶点并做上标记,开始走了噢!
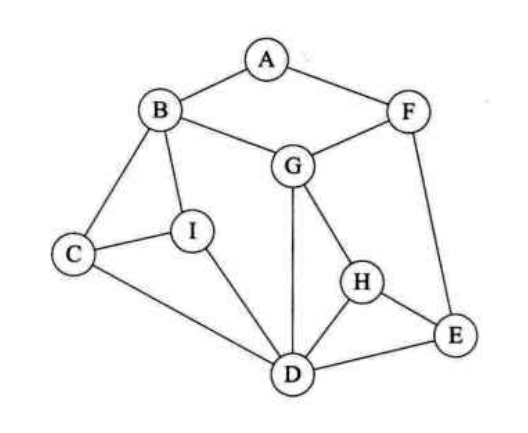
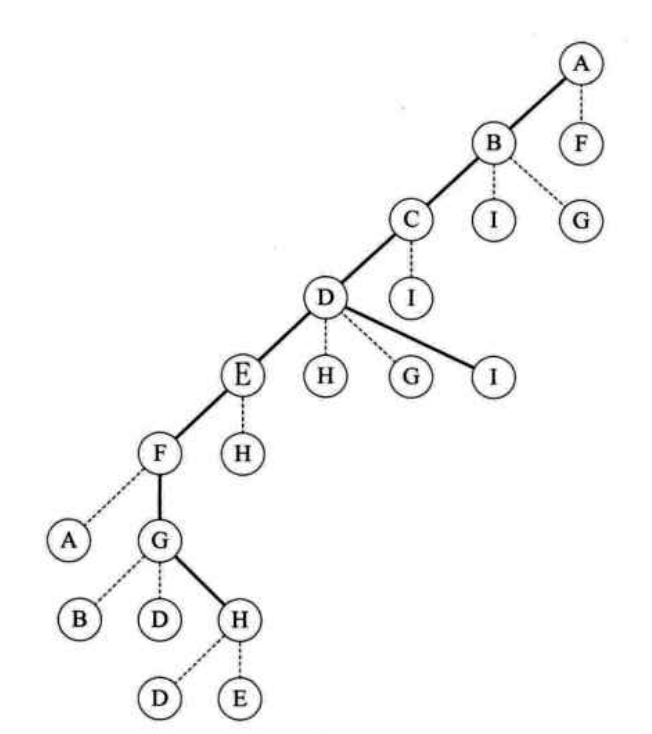
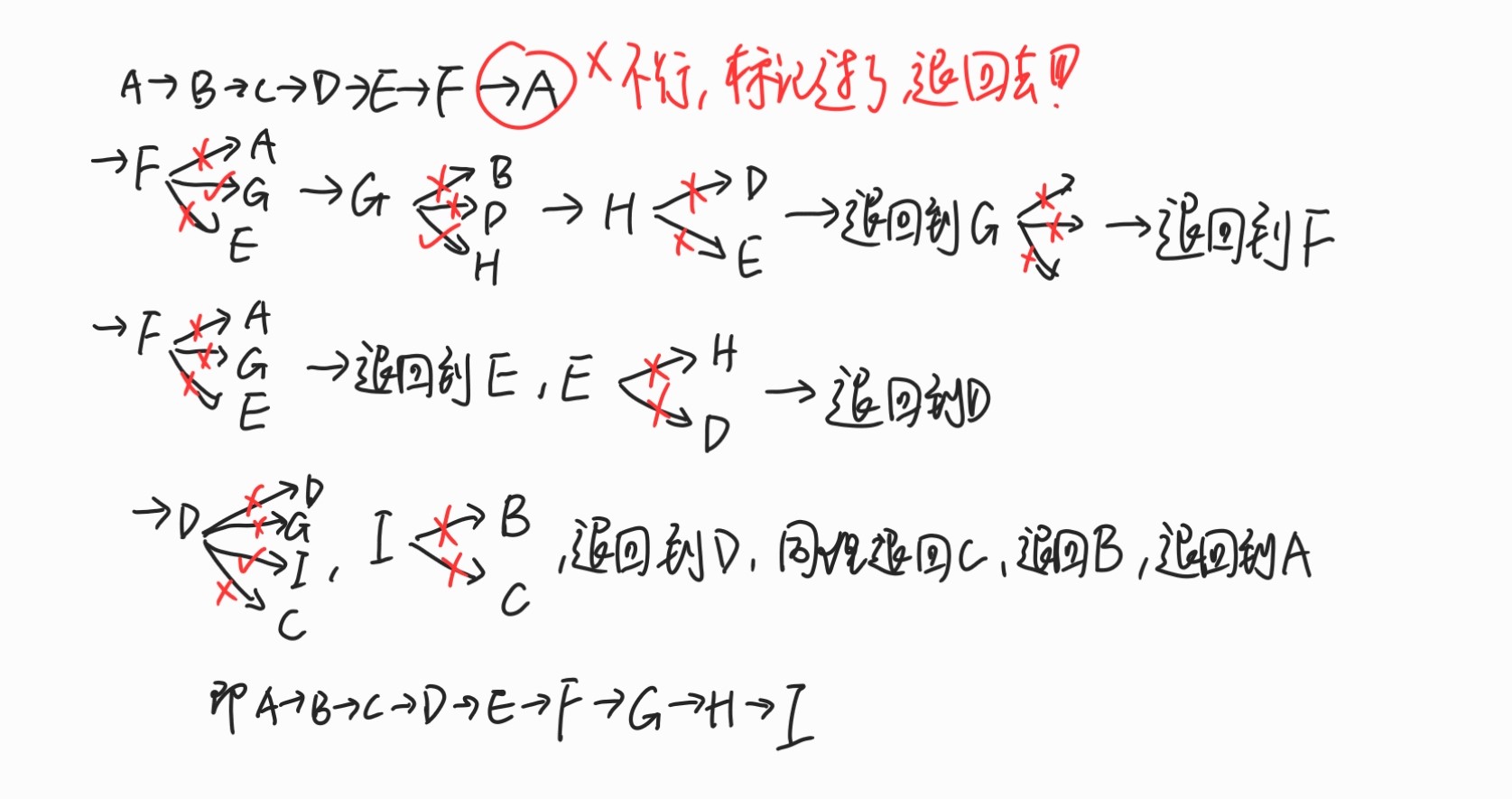
不难发现其实就是一个递归的过程,再细心观察,其实就是一棵树的前序遍历(先访问根结点,再左子树,再右子树)。
void DFS(int v,AGraph *G)
{
visit[v] = 1;
Visit(v);
ArcNode *q = G->adjList[v].first;
while(q != NULL)
{
if (visit[q->adjv] == 0)
DFS(q->adjv,G);
q = q->next;
}
}
图的遍历算法-广度优先搜索遍历(BFS)
图的广度优先遍历类似于树的层次遍历。
将之前那个图变一下形状:
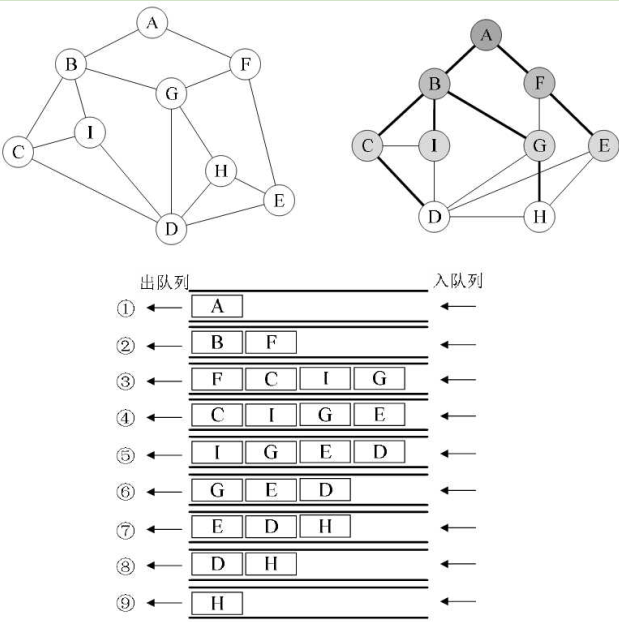
那么,从顶点A出发,则与A相邻的有B、F。(假如遵守右手原则),则是A→B→F。然后B又找到下一层CIG,F又找到下一层GE(但G已经被B遍历过有标记了),即为A→B→F→C→I→G→E,然后C找到下一层D,I找到下一层D(已标记),G找到下一层H,E找到下一层H,(已标记),所以为:A→B→F→C→I→G→E→D→H
void BFS(AGraph *G, int v, int visit[maxSize])
{
ArcNode *p;
int que[maxSize], front = 0 , rear = 0;
int j;
Visit(v);
Visit[v] = 1;
rear = (rear+1)%maxSize;
que[rear] = v;
while( front != rear)
{
front = (front+1)%maxSize;
j = que[front];
p = G->adjlist[j]first;
while( p != NULL)
{
if(visit[p->adjv] ==0)
{
visit[p->adjv];
visit[p->adjv] = 1;
rear = (rear + 1)%maxSize;
que[rear] = p->adjv;
}
p = p->next;
}
}
}
GS2-660-C5-58~61
这章蛮难的,很多细节和方法以及固定的思维定势要在这一章形成。加油
恋词U14
- essence n.本质;实质;精髓
- outlook n.景色;观点;世界观;人生观;展望,前景
- ritual n.(宗教等的)意识;例行公事 adj.作为仪式一部分的;例行的
- sacred adj.神圣的;宗教性的;庄严的
- preach v.宣讲;竭力鼓吹;说教;
- dean n.(圣公会)教长;大学的学院院长;系主任;训导主任
- pilgrim n.朝圣者;
- resemble v.像;类似于
- analogous adj.相似的;类似的
- stereotype n.模式化观念;刻板印象 v.对..产生成见
- conceal v.隐藏;隐瞒;掩盖
- zeal n.热情;热枕
- affiliation n.联系;从属关系
- filter n.过滤器;筛选程序; v.过滤;筛选
- dedicate v.奉献;把..用在
- verdict n.(陪审团的)裁定;裁决;判决;定论
- fall short of 未达到;不符合
- shorthand n.速记
- superfluous adj.过剩的;多余的
- superficial adj.表面的;肤浅的;浅薄的
- constitute v.组成;构成;被视为
- substitute n.代替者;代替物;替补 v.用..代替;取代
- readiness n.愿意;乐意;准备就绪