20210502

回顾

恋词复习

• affectionate adj.有感情的；慈爱的
• complementary adj.互为补充的；互补的
• thoroughly adv.十分地；彻底地
• permeate v.散步；传播；弥漫；渗透；渗入
• incorporate v.把..合并；使并入；混合；包含
• curriculum n.课程
• exploit v.开发；利用；剥削
• majestic adj.宏伟的；壮丽的；威严的
• hot stuff 性感的人；技艺很高的人
• deprive v.剥夺
• lest conj.唯恐；免得
• rival n.竞争对手 v.与..相匹敌；比得上 adj.竞争的；对立的

数据结构-树（二）

二叉树的定义

二叉树是n(n>=0)个结点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根结点和两棵互不相交的,分别称为根结点的左子树和右子树的二叉树组成。

其实就是对一般树加了些约束

• 每个结点最多两棵子树
• 子树有左右次序之分

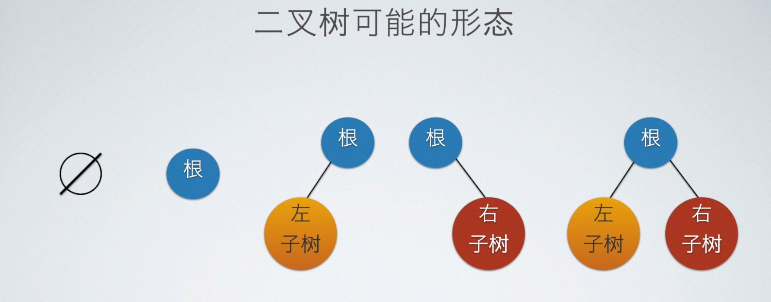
二叉树可能的形态

1. 空二叉树
2. 只有一个根结点
3. 根结点只有左子树
4. 根结点只有右子树
5. 树既有左子树也有右子树

满二叉树

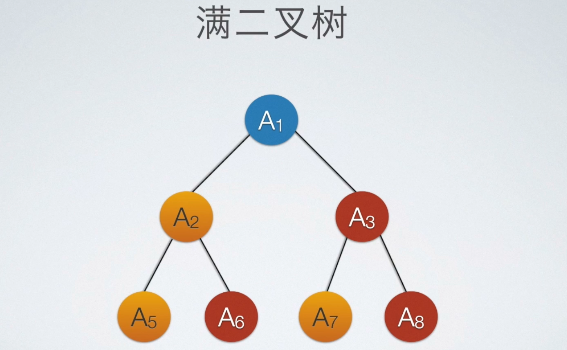
在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树。

满二叉树的特点:

1. 叶子只能出现在最下一层,出现在其他层就不可能达到平衡
2. 非叶子结点的度一定是2
3. 在同样深度的二叉树中,满二叉树的结点个数最多,叶子树最多

完全二叉树

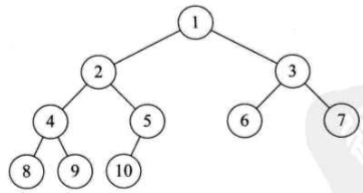
对一棵具有n个结点的二叉树按层序编号,如果编号为i(1<= i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,则这棵二叉树树完全二叉树。

其实就是由满二叉树挨个删除结点所得到的。如果跳着删除，得到的就不是完全二叉树。

完全二叉树的特点:

1. 叶子结点只能出现在最下两层
2. 最下层的叶子一定集中在左部连续位置
3. 倒数两层,若有叶子结点,一定都在右部连续位置
4. 若结点度为1,则该结点只有左孩子,即不存在只有右子树的情况
5. 同样结点树的二叉树,完全二叉树的深度最小

满二叉树一定是完全二叉树,而完全二叉树不一定是满二叉树

二叉树的性质

性质1

在二叉树的第i层上至多有$2^{i-1}$个结点(i>=1).

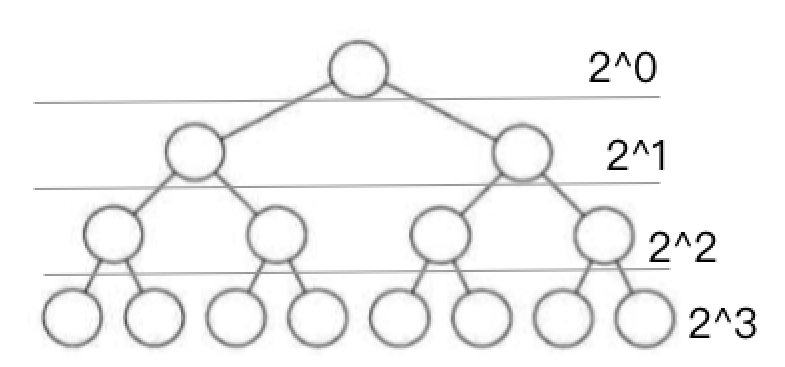
性质2

深度为k的二叉树至多有$2^k-1$个结点(k>=1).

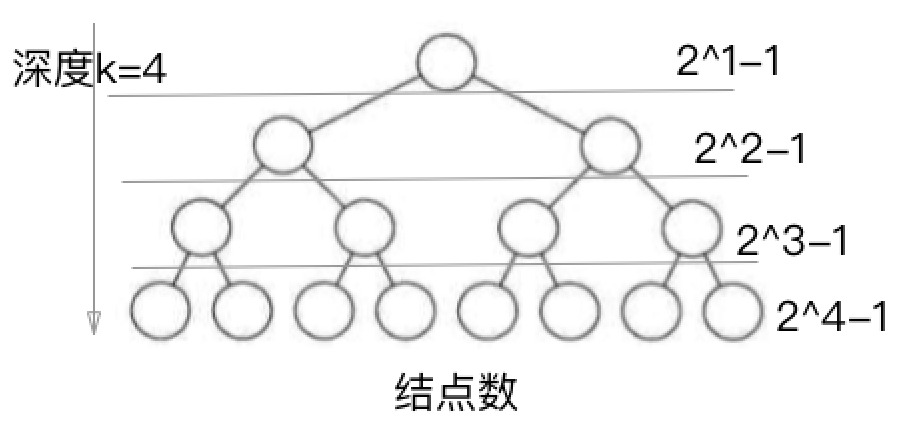
性质3

对任何一棵二叉树T,如果其终端结点数(叶子结点数)为$n_0$ ,度为2的结点数为$n_2$, ,则$n0 = n2＋1$

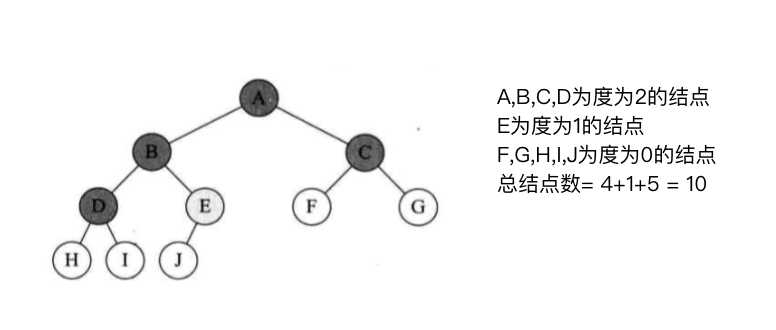
一棵二叉树中,除了叶子结点外剩下的就是度为1或2的结点树了,设n为度为1的结点数.则树的总结点数$n = n_0＋n_1+ n_2$

性质4

具有n个结点的完全二叉树的深度为$[log_{2}N]+1$或$log_{2}(n+1)$（|x|表示不大于x的最大整数）.

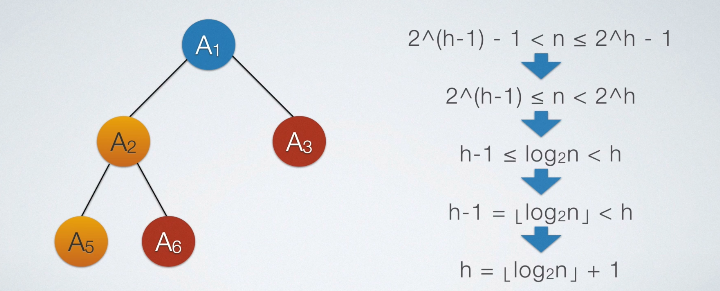
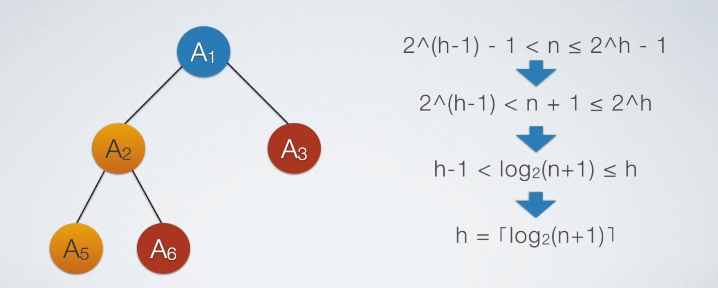
上图中最后两种表达都可以，选择题经常出现第二种。不同学校对于推导过程中等式的不同选择或者对于树的高度的不同规定，会出现不同高度表达式，要掌握推导方法！！

例题

分析：题目说第6层有8个叶结点，存在两种情况：（PS：叶结点只能出现在最下层和次下层）

1. 树总共6层：第六层只有8个结点，都是叶结点。
2. 树总共7层：但是第六层只有8个结点没有子结点，只能作为叶结点。

对于
①总共有：$2^5-1+8 = 39$个结点
②总共有 ：$2^6-1+(2^{6-1}-8)x2 = 63+48 = 111$个结点。

二叉树的顺序存储结构

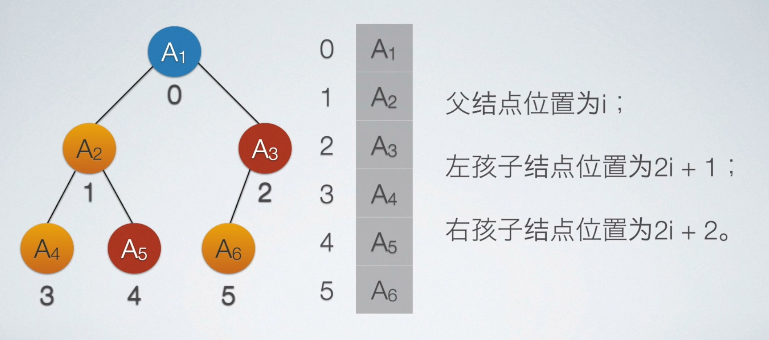
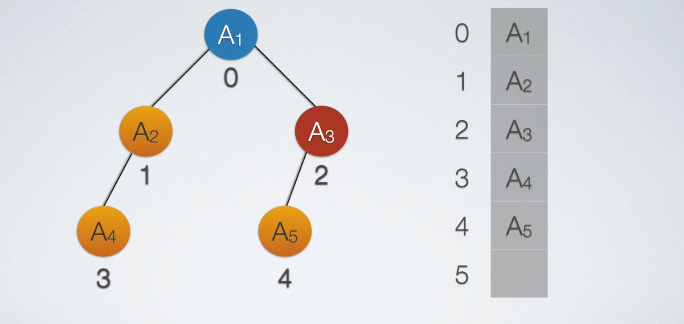
（上左图）这种存储结构只适合于完全二叉树，如果其他二叉树则不适用，如上右图。

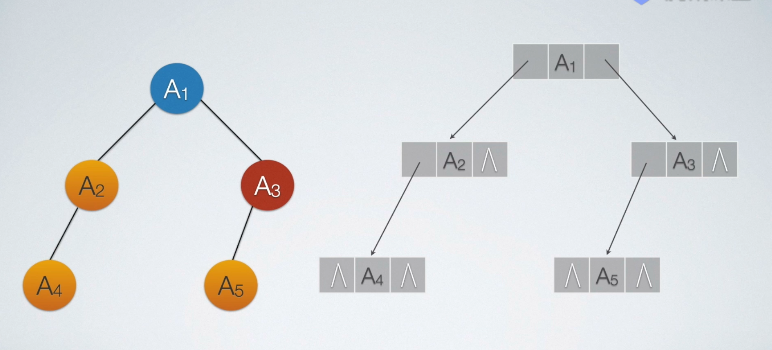
二叉树的链式存储结构（二叉链表存储结构）

二叉树每个结点最多有两个孩子,设计一个数据域和两个指针域,这样的链表为二叉链表。

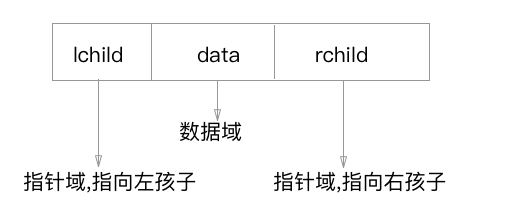
/* 二叉树的二叉链表结点结构定义 */
typedef struct BTNode        /* 结点结构 */    
{        
    int data;           /* 结点数据 */                      
    struct BTNode *lchild;
    struct BTNode *rchild; /* 左右孩子指针 */    
} BTNode;

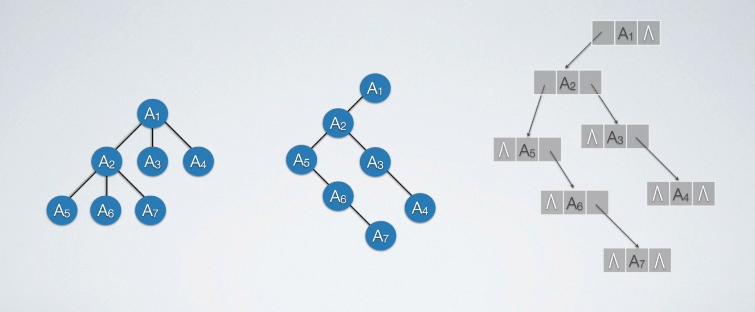
树的另外一种存储结构：孩子兄弟存储结构

typedef struct BTNode        /* 结点结构 */    
{        
    int data;           /* 结点数据 */                      
    struct BTNode* child;
    struct BTNode# sibling; /* 孩子兄弟指针 */    
} BTNode;

//链接
A1->child = A2;
A1->sibling = NULL;
A2->sibling = A3;
A3->sibling = A4;
A3->sibling = NULL;

//取A1孩子结点A3
A1->child->sibling