回顾
恋词复习
- perceive v.察觉;意识到;看作;认为
- receipt n.收据;收条;收到;接到
- hypocritical adj.伪善的;虚伪的
- decent adj.体面的,相当不错的;得体的;正派的
- incentive n.刺激;激励;鼓励;动机
数据结构-树(一)
定义
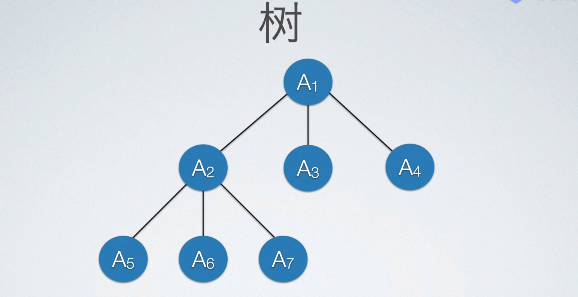
树(Tree) 是n(n≥0)个结点的有限集。n=0时称为空树。在任意一棵非空树中:
(1)有且仅有一个特定的称为 根(Root) 的结点;
(2)当n>1时,其余结点可分为m(m>0)个互不相交的有限集$T_1$、$T_2$、……、$T_m$,其中每一个集合本身又是一棵树,并且称为根的子树(SubTree)。
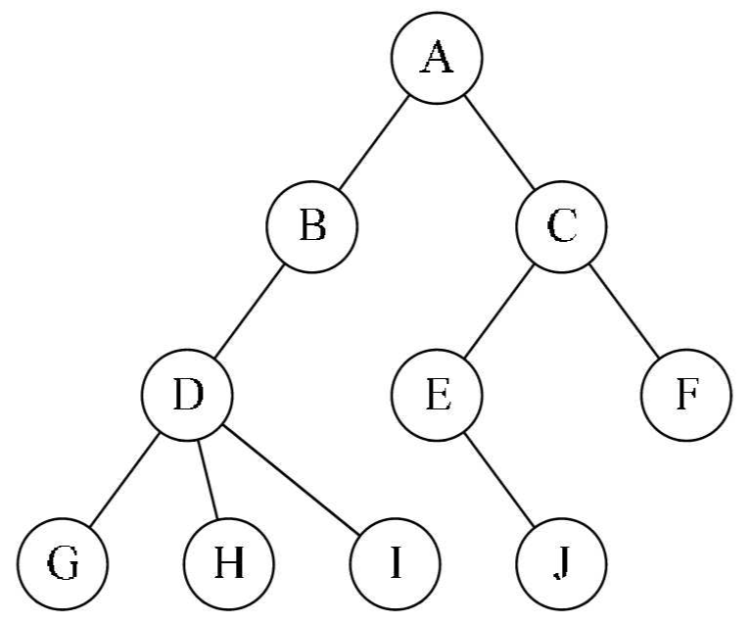
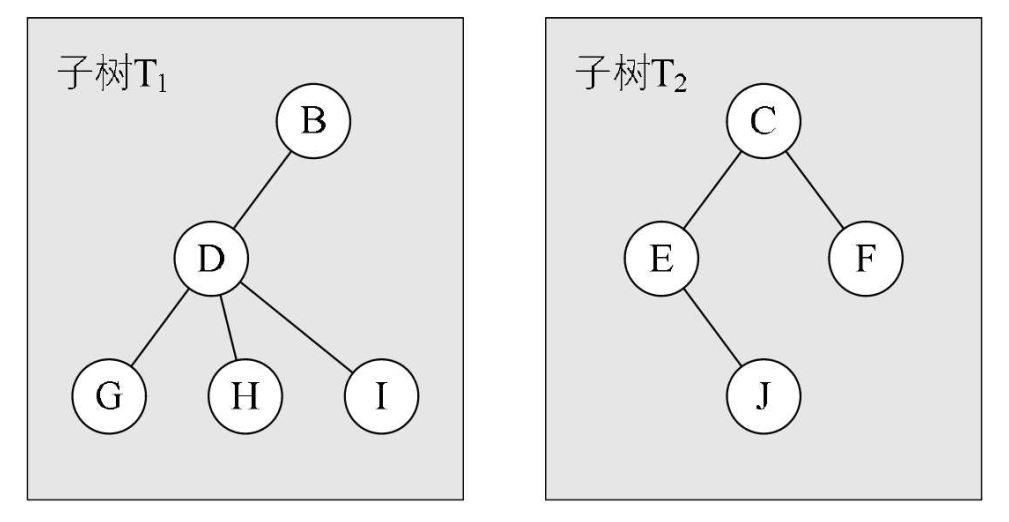
子树$T_1$和子树$T_2$就是根结点A的子树。D、G、H、I组成的树又是B为根结点的子树,E、J组成的树是以C为根结点的子树。
树的定义还要强调两点:
- n>0时根结点是唯一的,不可能存在多个根结点,
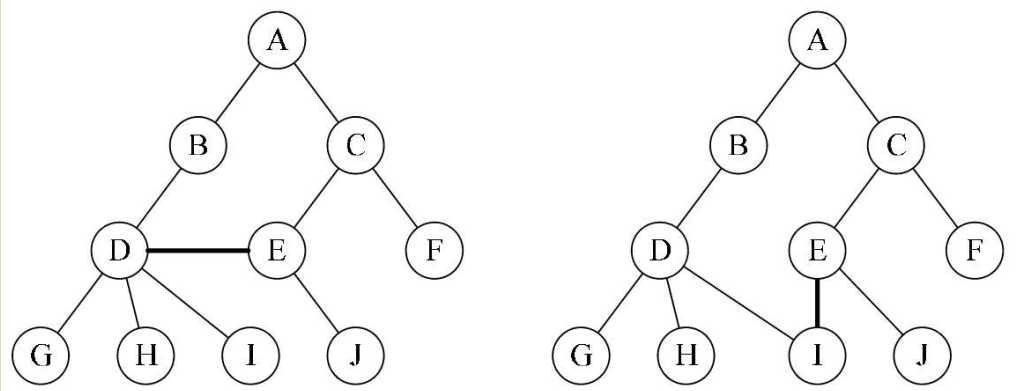
- m>0时,子树的个数没有限制,但它们一定是互不相交的。下图中的两个结构就不符合树的定义,因为它们都有相交的子树
结点分类
树的结点包含一个数据元素及若干指向其子树的分支。结点拥有的子树数称为结点的度(De-gree)。度为0的结点称为叶结点(Leaf) 或终端结点;度不为0的结点称为非终端结点或分支结点。除根结点之外,分支结点也称为内部结点。树的度是树内各结点的度的最大值。
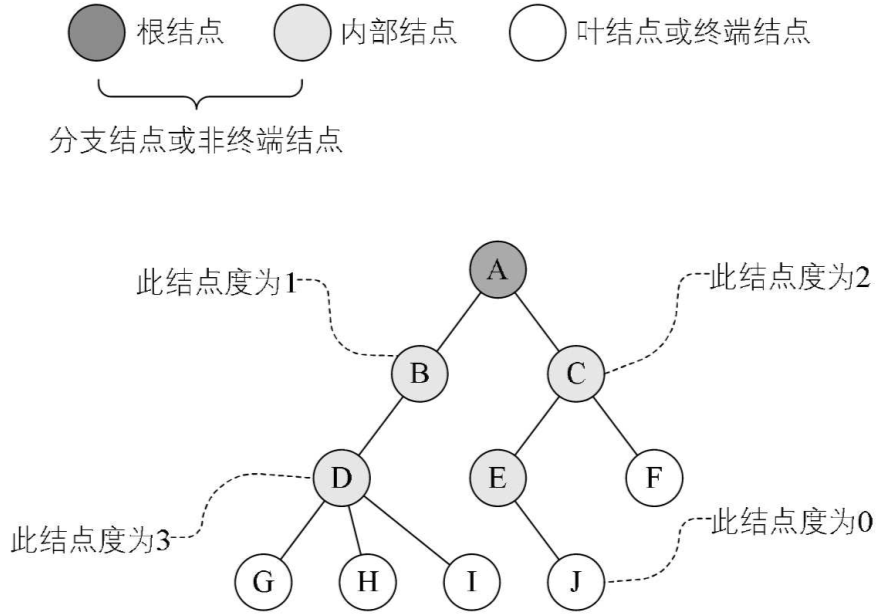
结点的度的最大值是结点D的度,为3,所以树的度也为3
结点间关系
结点的子树的根称为该结点的孩子(Child),相应地,该结点称为孩子的双亲(Parent),同一个双亲的孩子之间互称兄弟(Sibling)。结点的祖先是从根到该结点所经分支上的所有结点。以某结点为根的子树中的任一结点都称为该结点的子孙
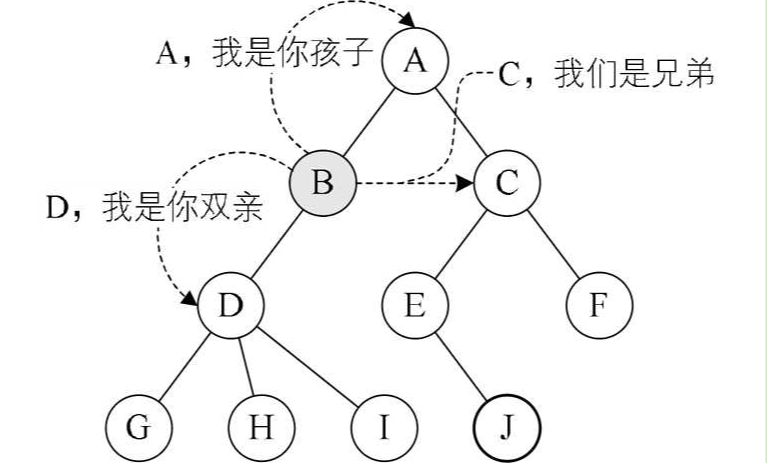
树的其他相关概念
结点的层次(Level) 从根开始定义起,根为第一层,根的孩子为第二层。若某结点在第i层,则其子树就在第i+1层。其双亲在同一层的结点互为堂兄弟。树中结点的最大层次称为树的深度(Depth)或高度
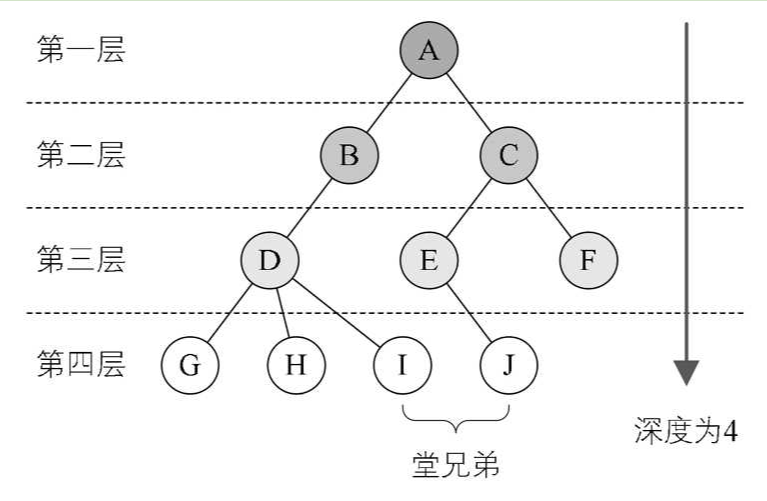
如果将树中结点的各子树看成从左至右是有次序的,不能互换的,则称该树为有序树,否则称为无序树。森林(Forest) 是m(m≥0)棵互不相交的树的集合。对树中每个结点而言,其子树的集合即为森林
线性表与树的结构:

例题
- 408,10年05题

度为4的树:
度:某个节点的子节点个数
叶结点:度为0的结点
度为4的树,说明该树中结点的子结点最多为4个
树中结点总个数=(所有的结点的度数)+1
∵ 在树中,除了根节点没有前驱结点,其他节点有且只有一个前驱结点(树的定义)
又∵ 父结点的‘度’是子结点的个数,而每个子结点前驱结点都是该父结点
∴ 因此,所有结点的“度”加起来,就是把所有结点子结点的个数加起来,又因为,根结点没有父节点,所以所以没有把根结点算计进来,于是:树中结点总个数=(所有的结点的度数)+1(根节点)
推广→ 一个森林的所有结点数=(所有结点的度数+n(n棵树,每棵树只有一个根节点)
->sum(所有结点个数)=20x4+10x3+1x2+10x1+1(根结点)=123个结点 ->sum(叶子节点个数)=123-20-10-1-10=82
- 例题

(1)可用根的生长法,一步步找出规律。如图:

(2)
什么时候最少?显然除第一层以外,其余每层k个结点的时候,总结点数最少,为1+k(h-1)个。
什么时候最多呢?即满k叉树情况,即每层结点数前后构成了等比数列:$1+k^{1}+k^{2}+k^{n-1} = k^{n-1}/k-1$
顺序存储结构
二叉树的顺序结构是用一维数组存储二叉树中的结点,并且结点的存储位置,也就是数组的下标要能体现结点之间的逻辑关系,比如双亲与孩子的关系,左右兄弟的关系。
双亲存储结构
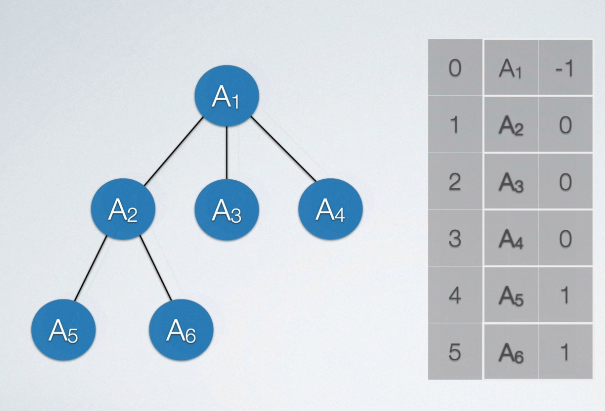
typedef struct
{
int data;
int pIdx;
}TNode;
TNode tree [maxsize];
tree[0].data = A1;
tree[0].pIdx = -l;
tree[1].data = A2;
tree[1].pIdx = 0;
tree[2].data = A3;
tree[2].pIdx = 0;
tree[3].data = A4;
tree[3].pIdx = 0;
tree[4].data = A5;
tree[4].pIdx = 1;
tree[5].data = A6;
tree[5].pIdx = A1;
简化形式(考研中常考形式):与数组下标对应(->数据元素)
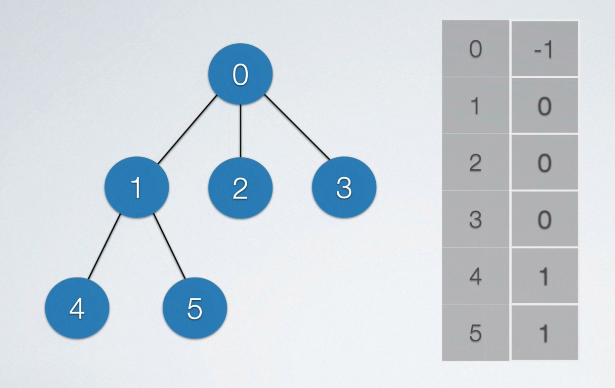
int tree[maxSize];
tree[0] = -l;
tree[1] = 0;
tree[2] = 0;
tree[3] = 0;
tree[4] = 1;
tree [5] =l;
链式存储结构
孩子存储结构和孩子兄弟存储结构。(孩子兄弟存储结构先不讲)
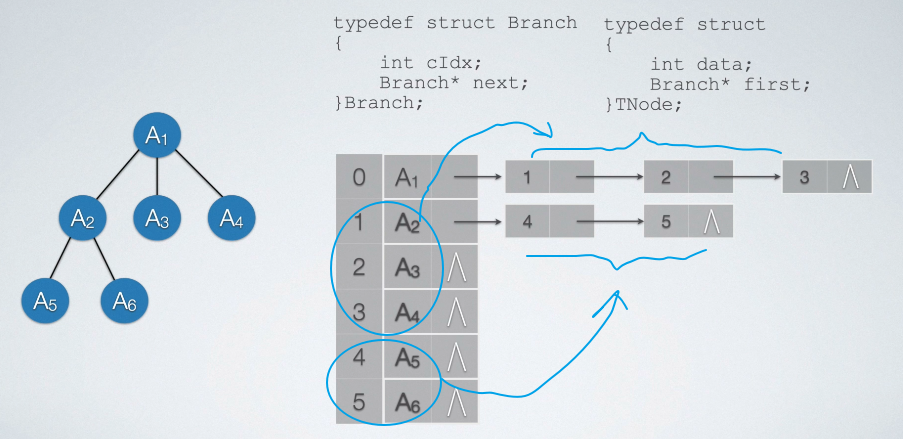
typedef struct Branch
{
int cIdx;
Branch* next;
}Branch;
typedef struct
{
int data;
Branch* first;
}TNode;