Table of Contents
回顾
数据结构-真题回顾
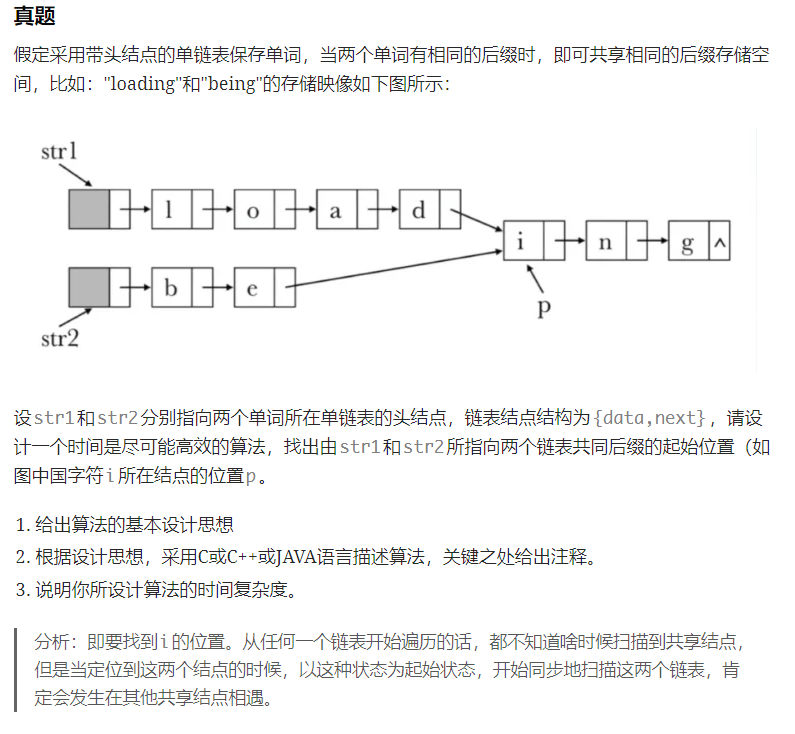
关于昨天的这个真题,昨晚回去想了一下发现有个问题。
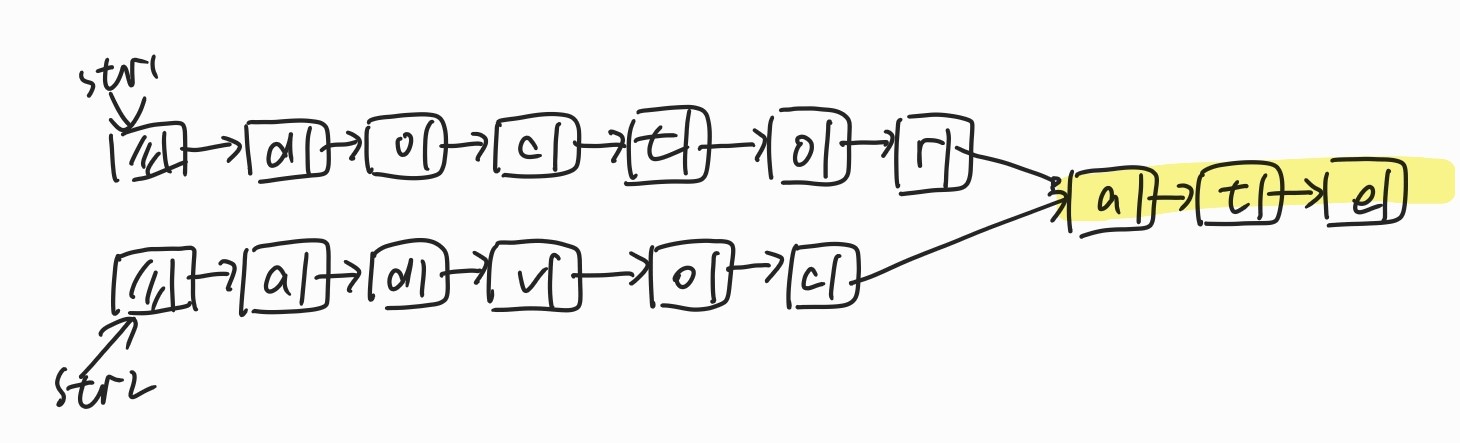
就是类似于doctorate和advocate这两个单词,在重复后缀ate存之前还是有一个字母重复:即o。我觉得如果遇到这种情况是不是就没有办法辨别是否是相同后缀,但实际上是我没有很好的理解题目的意思,我想的是左边的存储方式,但实际上是右边的存储方式。。
嗯,要读懂题目,只有这样才称之为重复的后缀。前面重复的不算。

恋词U1,U2,U3,U4,U5复习








多元函数微分学(一)
第一节:重极限 连续 偏导数 全微分
二元函数
二元函数的极限
- (x,y)->(x0,y0)是以“任意方式”。
- 一元函数极限中的下述性质对于多元函数仍然成立
- 局部有界性
- 保号性
- 有理运算
- 极限与无穷小的关系
- 夹逼性
- 洛必达已经不能使用了!!!
来看两个例题


- 多元函数求极限的方法因为没有了洛必达法则,所以相对来说考的难度也会相对降低。可以先用初步判断法判断函数的极限。
- 例1。分子三次,分母三次,那么极限很可能为0。对于极限为0的多元函数求极限的方法一般是“取绝对值用夹逼”。那么夹逼中不等式就可以写为:
,然后由夹逼定理就可得极限为0。
- 例2。分子两次,分母也是两次,那么极限很可能不存在。对于极限不存在的多元函数的证明方法一般是从多元函数的几何意义出发。找两条过原点且过
(x,y)的直线,然后代入,即可说明斜率不同即可。
- 例1。分子三次,分母三次,那么极限很可能为0。对于极限为0的多元函数求极限的方法一般是“取绝对值用夹逼”。那么夹逼中不等式就可以写为:
多元函数的连续性
记得与一元函数做对比噢!一元中关于连续性:1)定义 2)间断点及其类型 3)性质
- 连续的概念:还是那一点的极限等于那一点的函数值。
- 连续函数的性质
- 多元函数的和差积商(分母不为0)仍为连续函数
- 多元函数的复合函数也是连续函数
- 多元初等函数在其定义区域(≠定义域)内连续
- (最大值定理)有界闭区域D上的连续函数在区域D上必能取得最大值和最小值
- (介值定理)有界闭区域D上的连续函数在区域D上必能取得最大值与最小值之间的任何值。
偏导数
偏导数的定义

偏导数的几何意义
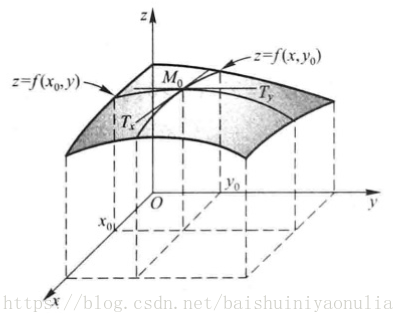
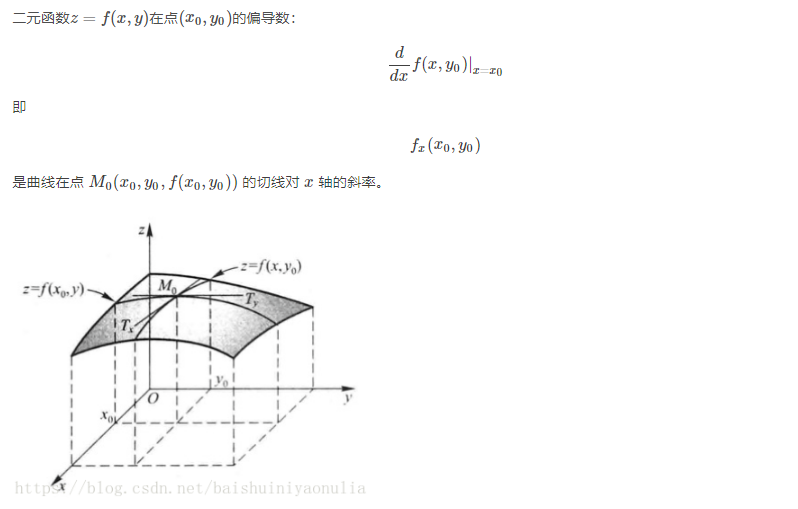

- 高阶偏导数

全微分



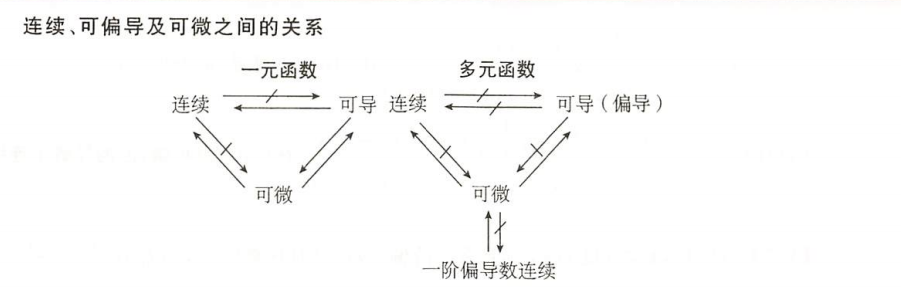
常考题型与例题
不在这里展示。