20210326

微分方程（二）| 数据结构-线性表（六）| 恋词U5

Table of Contents

微分方程（二）

常考题型与例题

具体题目不在这里展示了。

数据结构-线性表-表的逆置（六）

逆置就是把表中元素调整成与原来相反的位置。

顺序表逆置

上面两图都是顺序表的逆置示意图，不同的是要逆置的元素个数不同，左边为偶数，右边为奇数。但是相同的是，两种情况下当i<j的时候，逆置结束（循环结束），所以不用做算法区分。

for (int i = left, j = right; i < j; ++i,--j)

{

    tmep = a[i];

    a[i] = a[j];

    a[j] = temp;

}

单链表逆置

实现代码：

while(p->next != q)

{

    t = p->next;

    p->next = t->next;

    t->next = q->next;

    q->next = t;

}

例题

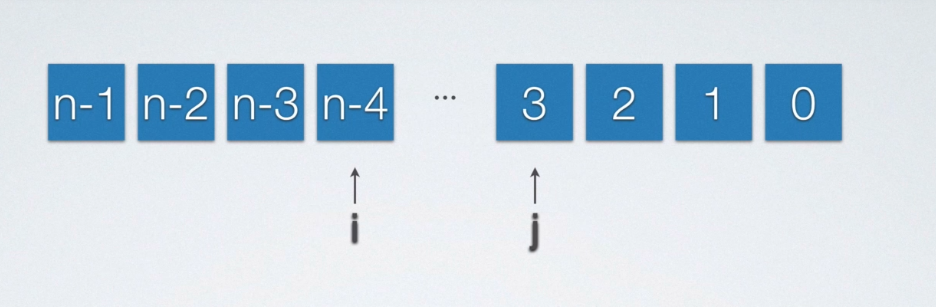
  1. 将一长度为n的数组的前端k(k<n)个元素逆序后移动到数组后端，要求原数组中数据不丢失，其余元素的位置无关紧要。

分析：其实就是顺序表的逆置问题，只是循环条件改一下即可，只扫描到k个位置即可。

image.png
image.png
void reverse(int a[], int left, int right, int k)

{

    int temp;

    for(int i = left,j = right; i < left + k && i<j; ++i; --j)

    {

         tmep = a[i];

     a[i] = a[j];

     a[j] = temp;

    }

}

注意：因为left+k有可能大于表长的一半，所以需要i<j。

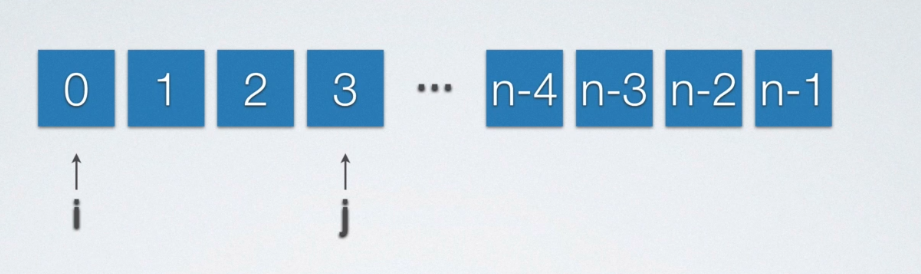
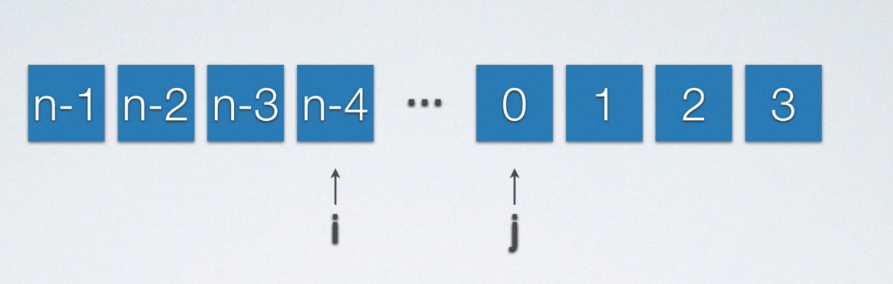
  1. 将一长度为n的数组的前端k(k<n)个元素保持原序移动到数组后端要求原数组中数据不丢失，其余元素的位置无关紧要。

最容易想到的算法就是利用某种算法将前k个元素与后k个元素交换即可，但是这里不采用这种算法。可以先把前面要移动的元素逆置，第二步将已逆置前k个元素逆置到后端。

image.png
image.png
image.png
image.png
void moveToEnd(int a[], int n, int k)

{

reverse(a,0,k-1,k);

    reverse(a,o,n-1,k);

}

408真题

将n(n>1)个整数存放到一维数组R中。试设计一个在时间和空间两方面都尽可能高效的算法。将R中保存的序列循环左移p(0<p<n)个位置，即将R中的元素(X0,X1..Xn-1)，经过移动后变成(Xp,Xp+1,..Xn-1,X0,X1,...Xp-1)。

(1) 给出算法的基本设计思想
(2) 根据设计思想，采用C或C++或JAVA语言描述算法，关键之处给出注释。
(3) 说明你所设计算法的时间复杂度和空间复杂度。

分析：只需将0~p-1位置的元素逆置，再将p~n-1位置的元素逆置，然后再将整个数组逆置即可。

1234567 //循环左移3位

4567123 //循环左移完毕

只需

123 -> 321    //将0~p-1位置元素逆置

4567 -> 7564  //将p~n-1位置元素逆置

3217654       //再将整个数组逆置

4567123       //完毕

答案

(1)其过程是将0~p-1位置的元素逆置，再将p~n-1位置的元素逆置，然后再将正数组逆置即可。 (2)

void reverse(int a[], int left, int right, int k)

{

    int temp;

    for(int i = left,j = right; i < left + k && i<j; ++i; --j)

    {

         tmep = a[i];

     a[i] = a[j];

     a[j] = temp;

    }

}



void moveP(int a[], int n, int p)

{

    revrese(a,o,p-1,p);

    revrese(a,p,n-1,n-p);

    reverse(a,0,n-1,n);

}

(3) 时间复杂度为：O(n)
空间复杂度为：O(1)

恋词U5

考研英语 考研高数 408数据结构