回顾
准备做常考例题与题型的时候,发现利用定积分定义求极限的题目不太懂,那么归根到底就是定积分的定义没搞懂。那么就是自学阶段,找到一个说的不错的文章。听完武忠祥老师之后我也再去听了杨超老师关于这部分的讲解,豁然开朗,复盘一下。
首先就是定义:什么是定积分。

那么定积分用公式表示就是: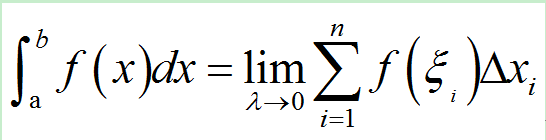
对于定积分的定义,我们知道有四个步骤:
分割、近似、求和、取极限。
其中,分割是任意的分割,想怎么分就怎么分,任意分!分割的目的在于第二步的代替。
代替什么呢?就是“化曲为直”,用直线来近似代替那段曲线,为什么这时候能够用直线来近似代替那段曲线了?就是因为第一步的分割呀!因为你第一步的分割分的让每个子区间足够小,小的让在小区间内随便取一点,代入到被积函数中,它的值都一样!既然都一样了,此时就可以将曲线看成直线了,此时这段小区间的面积就可以近似看作是小矩形的面积,宽就是小区间长度,长就是将这一点代入被积函数后的值。
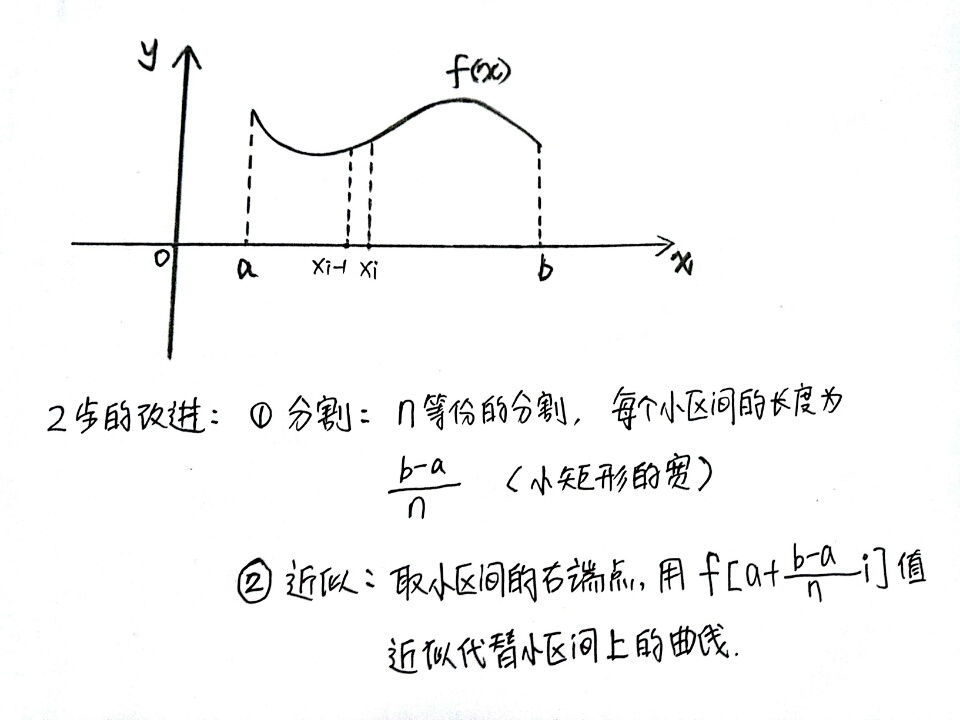
那么,考研里面对定积分的定义怎么考呢?这里借用杨超老师的言论:“考研里面是对定积分的定义做了两步的改进!”哪两步呢?就是第一步的分割和第二步的近似!

大家对照着上面的图一,看看上面讲的n等分法,这就是考研里面的特殊分割!你之前是任意分割,现在我就取个特殊,我将这个区间分成n等份,每一份的区间长度都是n分之一。
而近似呢,你之前的定义是说取小区间的任意一点,我这时候就取个特殊点,我取每个小区间的右端点!把这个右端点代入到被积函数中,用它的函数值来近似代替这段曲线上的每一点值,即:
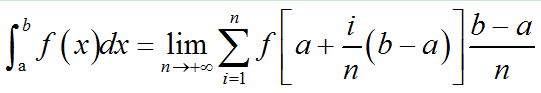
正是因为有了上面两步的特殊改进,才有了下面的0到1区间上的积分表达式:
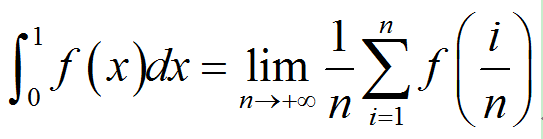
对于这个积分表达式!
你要想明白1/n代表什么?它代表的是矩形面积微元中的那个宽!
小f这个函数代表什么?它代表的是矩形面积微元中的那个长!
因此,对于若干项和的极限,你关注的焦点就是在这两个因子上!即提取配凑出这面积微元!
定积分(二)
常考题型与典型例题。
- 定积分的概念、性质及几何意义。
- 定积分的计算
- 变上限定积分
定积分的概念性质、性质及几何意义
- 例题1
。拿这道题来回顾一下定积分最重要的定义,嗯就是怎么去一步步求定积分的步骤!这部分很重要!,在上面回顾的时候已经重点复习了定积分的定义,那么其实这类利用定积分定义求和式极限的题目很多,但是都有比较一般的特点,就是:
- 分子齐(都是1次或0次);
- 分母齐(都是2次);
- 分母比分子多一次; 这道题除了可以用定积分定义做,当然也可以硬做,如图,要利用到之前提到的一个基本不等式:$x/(1+x) < ln(1+x) < x$。
而最简单的方法还是利用定积分的定义,将“可爱因子”提出。找原函数,简略答案如图:
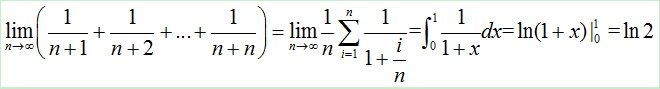 。
。
当然类似的题还有很多,比如: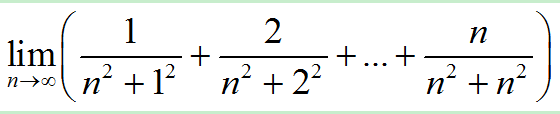
相同的方法,一样的逻辑。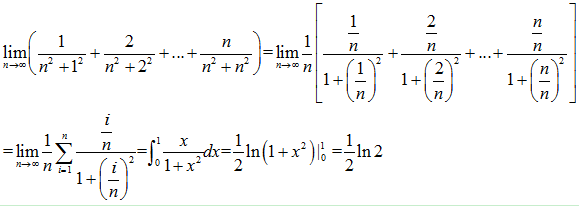
- 例题2,
,同样也是凑可爱因子,可是这题外面有个n,所以要往外提$1/n^2$才能凑到可爱因子,接下来就是找原函数,比较容易。
- 例题3,
。同理这道题也能看出是可以用用定积分定义所求的和式极限,那么这道题在凑可爱因子时,只需把其中一个$1/n$放进去,就可以凑得,从而找到原函数。
- 例题4,
,同样这道题也是求和式极限的一道题,把可爱因子提出即可得到原函数从而解决,比较容易!
背单词
- tropic 【n.回归线;热带 adj.热带的】
- snap 【v.突然断裂;噼啪作响;猛然咬;快速地 adj.突然的;匆忙的】
- invasion 【n.侵犯;侵略】
- bureaucracy 【n.官僚主义;官僚机构】