Jan 31, 2021

20210131

导数与微分（二）

有理运算法则，即“和差积商的导数”。
复合函数求导法-->链式求导法。
- 复习全书基础篇P34例6，运用有理运算法则中的乘法法则(uv)'=u'v+uv'即可。
- 复习全书基础篇P35例7，一个重要的结论：一个可导的奇偶函数求一次导数奇偶性发生一次变化，一个可导的周期函数求一次导依旧是周期函数。
- 复习全书基础篇P35例8，如果一步步去求导就太慢了，不难看出来f(x)是偶函数，那么求三次导之后是奇函数，奇函数在0点有定义，则此时o点的值即为0。（即运用了上面的那个结论。）
隐函数求导法：等式两边对x求导，把y看作为x的函数。
- 复习全书基础篇P35例9，等式两边对x求导即可（记住y是x函数的函数，y求导等于y'），然后把y'解出来即可。
反函数的导数：若y=f(x)可导，且f'(x)≠0，则其反函数x=φ(y)也可导，且φ'(y)=1/f'(x)，即反函数的导数等于原来导数的倒数。即。用几何上来解释比较清楚如下图

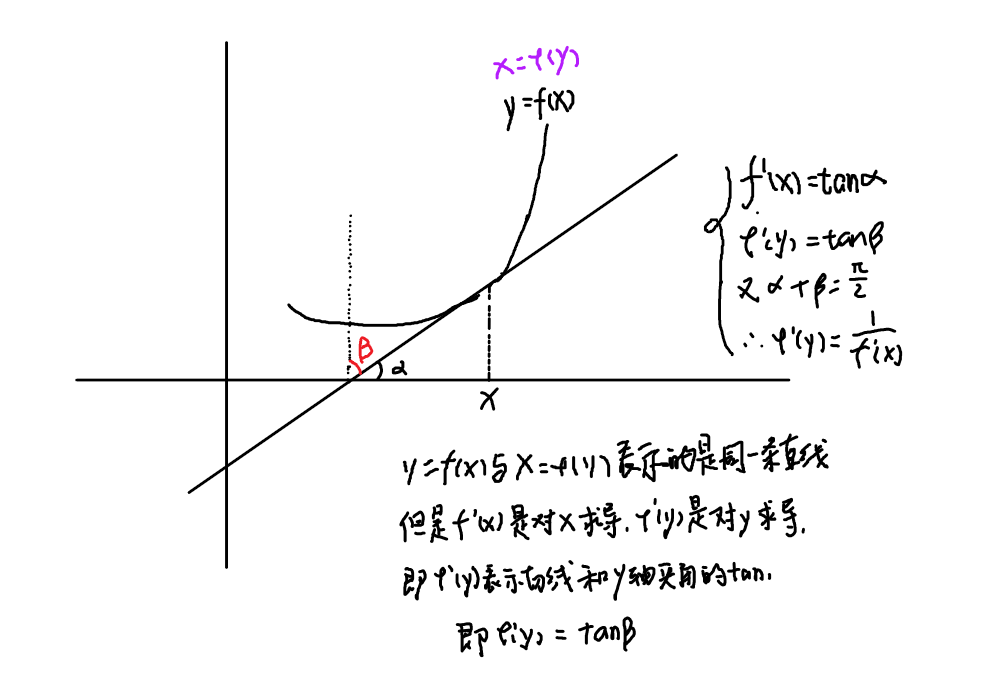
而复习全书基础篇P35例10可用这个结论，题目为证明：。那么令y=arcsinx，那么这个函数的反函数就为x=siny，又y∈(-Π/2,Π/2)，又(siny)'=cosy，所以φ'(y) = 1/cosy = 1/√1-sin²y(又因为x=siny)=1/√1-x²。

参数方程求导法：要搞清楚原理，在题目里面才不会出错。一般题目为求某参数方程确定的函数二阶导某个点的值。方法就是先求出一阶导，再求二阶导，再代点。值得注意的是，进行二阶导的时候并不是直接由一阶导的结果再对t求一次导，而是先对t求一次导，再乘以t对x求导！！看两道例题好好领悟一下。
- 复习全书基础篇P35例11,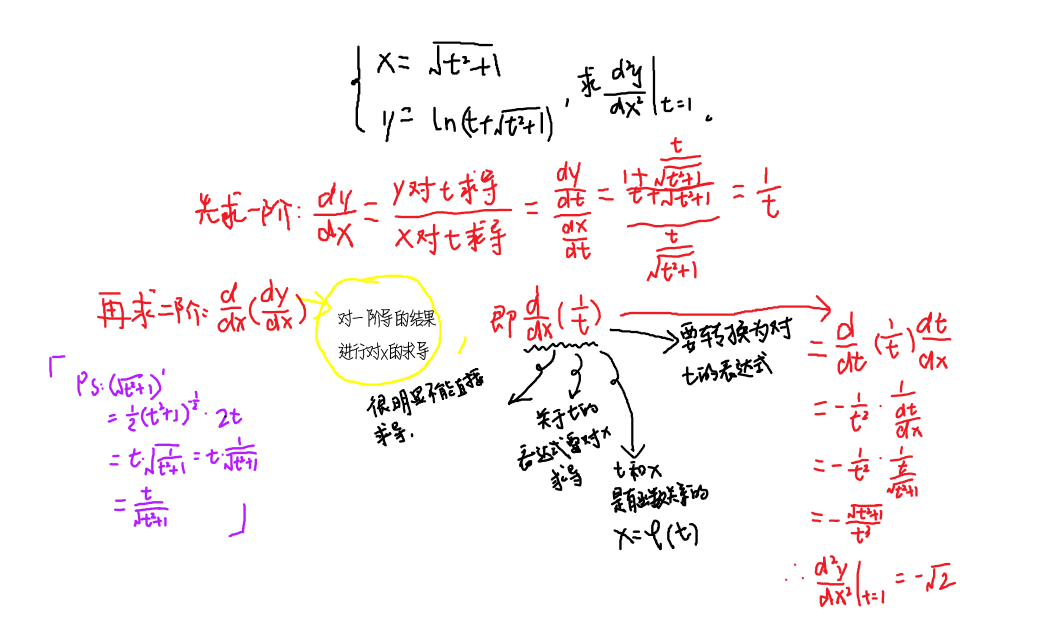
- 2015年数学2考题,
- 总结一下！先求一阶，求二阶别忘了乘以t对x的导数！
对数求导法，适用范围为多个函数的乘除和幂指函数的u(x)^v(x)的情形，具体方法就是将函数或者方程两边取对数，然后两边对x求导（运用隐函数求导法）。
- 复习全书基础篇P36例12，可以看出是u(x)^v(x)型，那么直接求导会很不方便，可以将，再两边对x求导（记住记住记住y是x的函数，所以y对x求导等于y'）。然后得到一个包含y，y'，x的等式接着解出y'即可。
- 复习全书基础篇P36例13，同理，两边取对数之后对x求导，求出y即可，别忘了等式中有y的要替换y的具体表达形式。